Comparando Algoritmos de Ordenação: Quem é o Mais Rápido? Uma Análise Prática de Desempenho

Introdução

Os algoritmos de ordenação estão entre os pilares da ciência da computação e são amplamente utilizados em inúmeras aplicações práticas. Desde a organização de dados para consultas rápidas até o processamento de informações em sistemas complexos, escolher o algoritmo de ordenação correto pode fazer uma enorme diferença no desempenho de um sistema.

Mas qual algoritmo é realmente o mais rápido? E como eles se comportam em diferentes volumes de dados? Para responder a essas perguntas, realizamos uma análise prática comparando seis algoritmos de ordenação populares: Bubble Sort, Selection Sort, Insertion Sort, Quick Sort, Merge Sort e Radix Sort. Cada um desses algoritmos tem uma abordagem única para organizar os dados, variando desde métodos mais simples, como o Bubble Sort, até abordagens mais sofisticadas, como o Quick Sort e o Merge Sort.

Esta análise não é apenas uma observação teórica das complexidades assintóticas, como $O(n^2)$ ou $O(n \, log \, n)$. Nosso foco é observar o desempenho real de cada algoritmo ao ordenar dados de diferentes tamanhos, desde pequenos conjuntos até grandes volumes. Ao comparar esses tempos de execução, conseguimos visualizar como os algoritmos se adaptam ao aumento de complexidade e volume.

Para tornar os resultados mais práticos, utilizamos dados numéricos gerados de maneira aleatória, simulando cenários comuns onde esses algoritmos seriam aplicados. Além disso, para otimizar o tempo de execução dos testes, rodamos cada algoritmo em paralelo utilizando o módulo concurrent.futures em Python, permitindo uma análise mais eficiente e comparativa de cada abordagem.

Objetivo do Estudo

Nosso objetivo é fornecer uma visão prática e visual sobre o desempenho dos algoritmos de ordenação mais comuns. Este estudo foi estruturado para responder a algumas questões-chave:

1. Qual algoritmo é o mais rápido em pequenos volumes de dados? Alguns algoritmos de ordenação são otimizados para conjuntos menores e podem ser a melhor escolha em determinadas situações.
2. Como os algoritmos escalam com o aumento de dados? Quando o volume de dados aumenta, a complexidade assintótica teórica dos algoritmos começa a impactar de forma mais visível o tempo de execução.
3. Quais algoritmos se tornam inviáveis com grandes volumes de dados? Algoritmos como o Bubble Sort e o Selection Sort, que têm complexidade $O(n^2)$, geralmente mostram desempenho ruim para volumes grandes.

Configuração do Ambiente de Teste

Para garantir que a análise de desempenho dos algoritmos de ordenação seja precisa e reprodutível, configuramos um ambiente de teste controlado em Python. A escolha da linguagem foi motivada pela sua simplicidade de implementação e pela vasta quantidade de bibliotecas para análise de dados e visualização de resultados. Nessa seção, vamos detalhar os passos seguidos para a criação do ambiente de teste, as ferramentas utilizadas e a metodologia adotada.

Tamanhos de Dados e Geração Aleatória

Para avaliar o desempenho dos algoritmos de ordenação, decidimos testar cada um com conjuntos de dados de tamanhos variados. Selecionamos os tamanhos 100, 500 e 1000 elementos, o que nos permitiu observar o comportamento de cada algoritmo tanto em pequenos conjuntos quanto em dados mais volumosos. Esse intervalo de tamanhos nos ajuda a entender como cada algoritmo se adapta ao aumento de complexidade.

Os dados foram gerados aleatoriamente utilizando a função random.sample() de Python, o que nos permitiu simular um cenário realista de dados não ordenados. Para assegurar que todos os algoritmos de ordenação processassem o mesmo conjunto de dados, geramos cada conjunto de dados uma única vez para cada tamanho e, em seguida, criamos cópias individuais para cada algoritmo, garantindo consistência nos testes.

Função de Medição de Tempo e Logs

Para medir o desempenho de cada algoritmo, utilizamos a função measure_time(), que registra o tempo de execução de cada algoritmo individualmente. Essa função registra o momento de início e término de cada ordenação usando time.perf_counter(), o que nos proporciona uma medição precisa do tempo decorrido.

Além de medir o tempo, adicionamos logs para indicar o início e o término de cada teste, o que nos permite acompanhar o progresso do experimento. Esses logs são especialmente úteis para conjuntos de dados maiores, onde alguns algoritmos, como o Bubble Sort, podem demorar mais.

Exemplo de código da função measure_time():

1def measure_time(sort_func, data, algo_name, size):
2    print(f"Iniciando {algo_name} para tamanho de dados: {size}")
3    start_time = time.perf_counter()
4    sort_func(data)
5    end_time = time.perf_counter()
6    duration = end_time - start_time
7    print(f"Concluído {algo_name} para tamanho de dados: {size} em {duration:.4f} segundos")
8    return duration

Execução dos Testes

Cada algoritmo foi testado individualmente para cada conjunto de dados. Abaixo está um exemplo do código que executa os testes:

1for size in data_sizes:
2    original_data = random.sample(range(size * 10), size)
3    
4    # Medindo o tempo de execução de cada algoritmo usando cópias do conjunto de dados original
5    results['Bubble Sort'].append(measure_time(bubble_sort, original_data.copy(), 'Bubble Sort', size))
6    results['Selection Sort'].append(measure_time(selection_sort, original_data.copy(), 'Selection Sort', size))
7    results['Insertion Sort'].append(measure_time(insertion_sort, original_data.copy(), 'Insertion Sort', size))
8    results['Quick Sort'].append(measure_time(quick_sort, original_data.copy(), 'Quick Sort', size))
9    results['Merge Sort'].append(measure_time(merge_sort, original_data.copy(), 'Merge Sort', size))
10    results['Radix Sort'].append(measure_time(radix_sort, original_data.copy(), 'Radix Sort', size))

Nesse código, para cada tamanho de dados, criamos uma cópia do conjunto original para cada algoritmo, garantindo que todos trabalhem com o mesmo conteúdo sem interferir uns nos outros. Dessa forma, conseguimos comparar o tempo de execução de forma justa entre os algoritmos.

Visualização dos Resultados

Para ilustrar o desempenho dos algoritmos de maneira clara e comparativa, usamos a biblioteca matplotlib para gerar gráficos de linha. Cada gráfico mostra o tempo de execução dos algoritmos em função do tamanho dos dados, permitindo uma visualização imediata de como o desempenho muda com o aumento do volume de dados. Algoritmos eficientes, como o Quick Sort e o Merge Sort, aparecem próximos ao eixo horizontal, enquanto algoritmos menos eficientes, como o Bubble Sort e o Selection Sort, apresentam uma curva acentuada, especialmente em conjuntos maiores.

Exemplo de código para plotagem:

1for algo, times in results.items():
2    plt.plot(data_sizes, times, label=algo)
3
4plt.xlabel("Tamanho do Dataset")
5plt.ylabel("Tempo de Execução (segundos)")
6plt.title("Comparação de Algoritmos de Ordenação")
7plt.legend()
8plt.show()

Descrição dos Algoritmos de Ordenação

Nesta seção, vamos explorar cada um dos algoritmos de ordenação testados, abordando suas características, sua complexidade teórica e os cenários onde eles são mais adequados. Cada algoritmo utiliza uma abordagem distinta para organizar os dados, o que resulta em variações de desempenho dependendo do volume e da natureza dos dados.

1. Bubble Sort

O Bubble Sort é um dos algoritmos de ordenação mais simples e, infelizmente, um dos menos eficientes em termos de complexidade de tempo. O seu funcionamento é baseado na comparação de pares de elementos adjacentes, trocando-os de posição quando estão na ordem errada. Esse processo é repetido até que toda a lista esteja ordenada.

• Complexidade de Tempo: $O(n^2)$ no pior e no caso médio, e $O(n)$ no melhor caso (quando a lista já está ordenada).
• Complexidade de Espaço: $O(1)$, pois é um algoritmo de ordenação in-place.
• Aplicabilidade: É mais adequado para conjuntos de dados muito pequenos ou para listas que estão quase ordenadas. Em listas grandes, seu desempenho é significativamente inferior aos outros algoritmos.

O Bubble Sort é simples de implementar, mas sua complexidade $O(n^2)$ significa que ele não é ideal para grandes volumes de dados, como veremos nos resultados.

2. Selection Sort

O Selection Sort também é um algoritmo simples, mas usa uma abordagem diferente do Bubble Sort. Ele procura o menor elemento da lista e o coloca na primeira posição. Em seguida, procura o segundo menor elemento e o coloca na segunda posição, repetindo esse processo até que a lista esteja ordenada.

• Complexidade de Tempo: $O(n^2)$ no pior, médio e melhor caso.
• Complexidade de Espaço: $O(1)$, pois também é um algoritmo de ordenação in-place.
• Aplicabilidade: Assim como o Bubble Sort, é adequado para listas pequenas, mas geralmente é um pouco mais eficiente que o Bubble Sort em prática.

Apesar de sua simplicidade, o Selection Sort também sofre com a complexidade $O(n^2)$, tornando-o ineficiente para conjuntos de dados maiores.

3. Insertion Sort

O Insertion Sort é uma escolha popular para listas pequenas ou parcialmente ordenadas. O algoritmo percorre a lista de dados e insere cada elemento na posição correta dentro de uma sublista crescente, que começa com apenas o primeiro elemento.

• Complexidade de Tempo: $O(n^2)$ no pior caso, mas $O(n)$ no melhor caso (quando a lista já está ordenada).
• Complexidade de Espaço: $O(1)$, pois é um algoritmo de ordenação in-place.
• Aplicabilidade: Desempenha bem em listas pequenas e é uma boa opção para listas quase ordenadas.

O Insertion Sort é consideravelmente mais rápido que o Bubble e o Selection Sort em listas que estão parcialmente ordenadas ou são pequenas.

4. Quick Sort

O Quick Sort é um dos algoritmos de ordenação mais populares devido ao seu desempenho médio excelente. Ele usa uma abordagem de divisão e conquista, escolhendo um elemento como pivô e dividindo a lista em duas sublistas: uma com elementos menores que o pivô e outra com elementos maiores. O processo é repetido recursivamente para cada sublista até que a lista inteira esteja ordenada.

• Complexidade de Tempo: $O(n \, log \, n)$ no caso médio e melhor caso, e $O(n^2)$ no pior caso (ocorre quando o pivô escolhido é o menor ou o maior elemento em cada partição).
• Complexidade de Espaço: $O(log \, n)$ no caso médio devido à recursão.
• Aplicabilidade: É adequado para a maioria das listas e é geralmente mais rápido que o Merge Sort e o Heap Sort em prática.

Apesar do risco de cair no pior caso, o Quick Sort é amplamente usado pela sua eficiência no caso médio e pela possibilidade de ser otimizado com boas escolhas de pivô.

5. Merge Sort

O Merge Sort é um algoritmo de divisão e conquista que divide a lista em duas partes, ordena cada uma delas recursivamente e, em seguida, as combina em uma lista ordenada. Diferente do Quick Sort, o Merge Sort tem uma complexidade de tempo garantida de $O(n \, log \, n)$ em todos os casos.

• Complexidade de Tempo: $O(n \, log \, n)$ no pior, médio e melhor caso.
• Complexidade de Espaço: $O(n)$, pois requer espaço adicional para combinar as sublistas ordenadas.
• Aplicabilidade: É uma excelente escolha para listas grandes ou quando a estabilidade é necessária.

Embora o Merge Sort seja mais consistente que o Quick Sort, ele consome mais memória, o que pode ser um fator limitante em ambientes com pouca memória.

6. Radix Sort

O Radix Sort é um algoritmo de ordenação não-comparativo que é particularmente eficiente para ordenar inteiros grandes. Ele classifica os elementos por dígitos, começando pelo dígito menos significativo até o mais significativo. Esse processo torna o Radix Sort muito eficiente para listas de inteiros grandes, em que a quantidade de dígitos (ou o comprimento dos números) é pequena em comparação ao número de elementos.

• Complexidade de Tempo: $O(nk)$, onde n é o número de elementos e k é o número de dígitos máximos dos elementos.
• Complexidade de Espaço: $O(n + k)$.
• Aplicabilidade: Ideal para listas de inteiros, especialmente quando o intervalo dos valores é limitado.

Diferente dos outros algoritmos comparativos, o Radix Sort é linear em relação ao número de elementos e é extremamente eficiente para grandes listas de números inteiros.

Análise dos Resultados

Para visualizar o desempenho de cada algoritmo de ordenação, criamos gráficos que comparam o tempo de execução em diferentes tamanhos de dados: 100, 500, 1000, 5000, 10000 e 50000 elementos. Esses gráficos revelam como os algoritmos escalam em relação ao aumento do volume de dados, evidenciando a complexidade de cada um e os cenários onde eles se destacam ou se tornam inviáveis.

Gráfico 1: Desempenho para Conjuntos Pequenos (100 a 1000 Elementos)

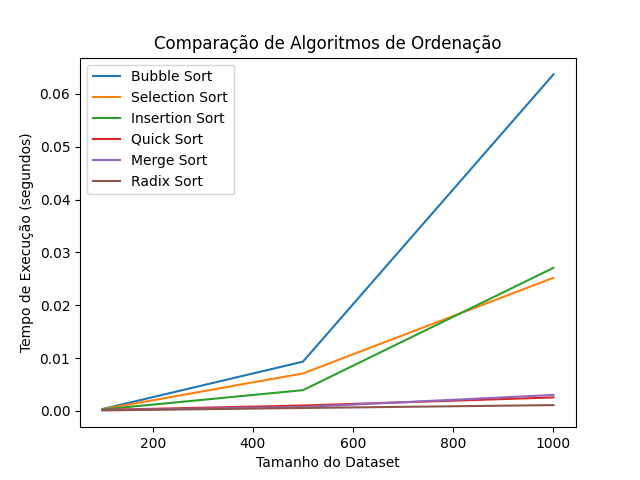
No primeiro gráfico, analisamos o desempenho dos algoritmos com conjuntos de dados pequenos, variando de 100 a 1000 elementos. Neste intervalo, os algoritmos de complexidade $O(n^2)$, como Bubble Sort, Selection Sort e Insertion Sort, ainda conseguem completar a ordenação em tempos relativamente baixos, embora já comecem a mostrar diferenças significativas em relação aos algoritmos mais rápidos.

• Bubble Sort: Como esperado, o Bubble Sort foi o algoritmo mais lento no conjunto de testes. Mesmo em 1000 elementos, ele já apresenta um tempo de execução consideravelmente mais alto do que os outros.
• Selection Sort e Insertion Sort: Ambos tiveram desempenho ligeiramente melhor que o Bubble Sort, mas ainda se mostram ineficientes em comparação com algoritmos mais otimizados.
• Quick Sort e Merge Sort: Esses algoritmos, com complexidade $O(n \, log \, n)$, já se destacam aqui, completando a ordenação quase instantaneamente. O Quick Sort, em particular, foi consistentemente o mais rápido nos testes com esses tamanhos de dados.
• Radix Sort: O Radix Sort também apresentou um excelente desempenho, mostrando sua eficiência em listas de números inteiros. Ele completou a ordenação rapidamente em todos os tamanhos testados.

Este gráfico mostra que, mesmo para conjuntos menores, algoritmos como Quick Sort, Merge Sort e Radix Sort são significativamente mais rápidos, e que o Bubble Sort deve ser evitado em favor de outras opções.

Gráfico 2: Desempenho para Conjuntos Médios (1000 a 5000 Elementos)

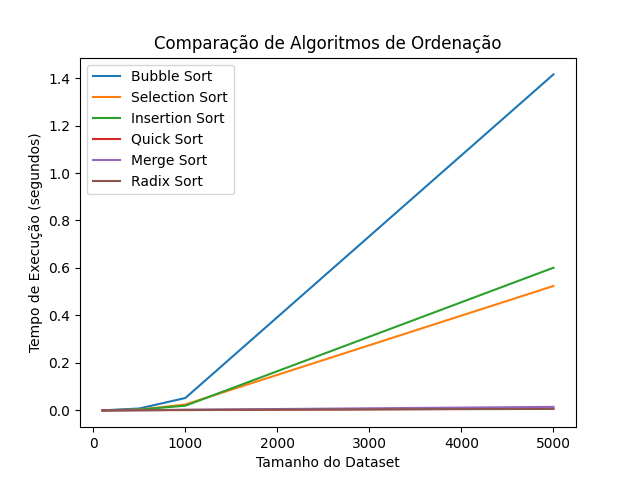
No segundo gráfico, ampliamos o conjunto de dados para tamanhos de até 5000 elementos. Aqui, as diferenças de desempenho entre os algoritmos ficam ainda mais claras, e a complexidade dos algoritmos começa a se refletir de forma mais acentuada no tempo de execução.

• Bubble Sort: Com 5000 elementos, o Bubble Sort já se torna praticamente inviável, levando um tempo considerável para completar a ordenação.
• Selection Sort e Insertion Sort: Estes algoritmos também enfrentam dificuldades em lidar com tamanhos maiores. Embora o Insertion Sort seja um pouco mais rápido que o Selection Sort em algumas circunstâncias, ambos mostram um aumento substancial no tempo de execução.
• Quick Sort e Merge Sort: Com complexidade $(n \, log \, n)$, esses algoritmos continuam apresentando excelente desempenho, completando a ordenação de 5000 elementos rapidamente.
• Radix Sort: O Radix Sort ainda se destaca, completando a ordenação quase no mesmo tempo que o Quick Sort e o Merge Sort. Isso reforça sua eficiência em listas de inteiros, especialmente quando comparado aos algoritmos de complexidade $O(n^2)$.

Esse gráfico evidencia que, para conjuntos de dados de tamanho médio, os algoritmos de complexidade $O(n \, log \, n)$ (Quick Sort e Merge Sort) e o Radix Sort são as melhores escolhas. Algoritmos como Bubble Sort e Selection Sort não são recomendados, pois a diferença de tempo de execução se torna considerável.

Gráfico 3: Desempenho para Conjuntos Grandes (1000 a 50000 Elementos)

No terceiro gráfico, que cobre até 50000 elementos, a diferença entre os algoritmos se torna ainda mais evidente. Aqui, algoritmos de complexidade O(n²) são extremamente lentos, enquanto algoritmos de complexidade O(n log n) e o Radix Sort se mostram capazes de lidar com grandes volumes de dados.

• Bubble Sort: O tempo de execução do Bubble Sort se torna proibitivo, ultrapassando a marca de vários minutos. Este resultado confirma que ele não é adequado para conjuntos grandes.
• Selection Sort e Insertion Sort: Embora apresentem uma melhora em relação ao Bubble Sort, ambos ainda levam um tempo significativo para ordenar 50000 elementos, tornando-se inviáveis para conjuntos dessa magnitude.
• Quick Sort e Merge Sort: O Quick Sort continua sendo um dos algoritmos mais rápidos, completando a ordenação em uma fração do tempo necessário para os algoritmos $O(n^2)$. O Merge Sort, apesar de ligeiramente mais lento que o Quick Sort, também se mantém eficiente em grandes volumes de dados.
• Radix Sort: O Radix Sort novamente se destaca, especialmente para grandes volumes de dados inteiros. Ele foi capaz de competir diretamente com o Quick Sort e, em alguns casos, foi ainda mais rápido, graças à sua complexidade linear em relação ao número de dígitos.

Esse gráfico confirma que, para conjuntos de dados grandes, o Radix Sort, o Quick Sort e o Merge Sort são as melhores opções. O desempenho desses algoritmos é estável e eficiente, enquanto algoritmos como Bubble Sort, Selection Sort e Insertion Sort devem ser evitados.

Resumo dos Resultados

A análise gráfica mostra claramente que a complexidade teórica dos algoritmos se reflete no desempenho prático. Os algoritmos de complexidade O(n²) — Bubble Sort, Selection Sort e Insertion Sort — rapidamente se tornam inviáveis à medida que o tamanho dos dados cresce. Por outro lado, algoritmos como o Quick Sort e o Merge Sort, com complexidade O(n log n), demonstram um desempenho estável e eficiente mesmo para grandes volumes de dados.

O Radix Sort se destaca particularmente para listas de inteiros, confirmando sua eficiência em conjuntos de dados grandes. Isso ocorre porque o Radix Sort não depende de comparações, o que permite que ele opere em tempo quase linear em relação ao número de elementos e à quantidade de dígitos dos números.

Na próxima seção, faremos uma comparação entre a complexidade teórica dos algoritmos e o desempenho prático observado, explorando como esses resultados se relacionam e quando é recomendável usar cada algoritmo.

Comparação da Complexidade Teórica com Resultados Práticos

A complexidade de um algoritmo é uma métrica teórica que permite estimar como o tempo de execução (ou o espaço necessário) cresce conforme o número de elementos na entrada aumenta. Na prática, a complexidade de um algoritmo pode nos ajudar a prever quais algoritmos terão melhor desempenho em diferentes tamanhos de dados, mas fatores como otimizações internas e o tipo de dados também podem impactar os resultados reais.

Nesta seção, vamos comparar a complexidade teórica de cada algoritmo com os tempos de execução observados nos testes práticos, analisando quando essas previsões se confirmam e onde elas podem diferir dos resultados reais.

Algoritmos de Complexidade $O(n^2)$: Bubble Sort, Selection Sort e Insertion Sort

Os algoritmos de complexidade $O(n^2)$ — Bubble Sort, Selection Sort e Insertion Sort — têm em comum o fato de que o número de operações cresce rapidamente à medida que o tamanho do conjunto de dados aumenta. Em outras palavras, para cada elemento adicional, o trabalho do algoritmo aumenta exponencialmente.

Comparação Teórica vs. Prática:

• Bubble Sort foi o mais lento dos três em todos os cenários, como previsto pela sua complexidade. Esse algoritmo, que é baseado em trocas de posições adjacentes, apresenta um número de comparações e trocas que cresce drasticamente conforme o tamanho dos dados aumenta.
• Selection Sort também apresentou tempos elevados, embora tenha sido ligeiramente mais rápido que o Bubble Sort na maioria dos casos. Na teoria, ambos têm a mesma complexidade, mas o Selection Sort evita algumas trocas desnecessárias, o que o torna mais eficiente em certos casos.
• Insertion Sort é um pouco mais eficiente que o Bubble Sort e o Selection Sort para listas parcialmente ordenadas ou pequenas. Isso é consistente com sua complexidade $O(n)$ no melhor caso, quando a lista está quase ordenada. No entanto, conforme o volume de dados cresce, ele também se torna inviável para conjuntos grandes.

Esses resultados confirmam a previsão teórica de que algoritmos de complexidade $O(n^2)$ são inadequados para conjuntos de dados grandes. Em casos práticos, esses algoritmos são viáveis apenas para listas muito pequenas ou para dados que já estão quase ordenados.

Algoritmos de Complexidade $O(n \, log \, n)$: Quick Sort e Merge Sort

Os algoritmos de complexidade $O(n \, log \, n)$, como Quick Sort e Merge Sort, foram projetados para realizar menos operações em média, tornando-os mais adequados para grandes volumes de dados. Essa complexidade implica que, mesmo com o aumento do volume de dados, o tempo de execução cresce de maneira mais controlada do que nos algoritmos de $O(n^2)$.

Comparação Teórica vs. Prática:

• Quick Sort foi consistentemente um dos algoritmos mais rápidos nos testes práticos. Ele tem um caso médio de complexidade $O(n \, log \, n)$, o que explica seu bom desempenho, mas seu pior caso é $O(n^2)$. Felizmente, na prática, o Quick Sort raramente atinge o pior caso, especialmente quando o pivô é escolhido com inteligência. Em nossos testes, ele manteve um desempenho excelente em todos os tamanhos de dados.
• Merge Sort também apresentou um desempenho consistente, com uma complexidade garantida de $O(n \, log \, n)$ em todos os casos. Ao contrário do Quick Sort, ele não corre o risco de cair no pior caso $O(n^2)$, tornando-o uma escolha segura para dados de qualquer tamanho. Porém, o Merge Sort tem uma desvantagem: ele requer espaço extra para combinar as sublistas, o que pode ser uma limitação em sistemas com pouca memória.

Os testes práticos confirmam a previsão teórica de que algoritmos $O(n \, log \, n)$ são eficientes e escaláveis. O Quick Sort foi ligeiramente mais rápido que o Merge Sort na maioria dos cenários, mas o Merge Sort é mais previsível em termos de desempenho e não depende de escolhas de pivô para manter sua eficiência.

Algoritmo de Complexidade $O(nk)$: Radix Sort

O Radix Sort é um algoritmo de ordenação não-comparativo com complexidade $O(nk)$, onde n é o número de elementos e k é o número máximo de dígitos dos elementos. Essa complexidade linear é especialmente vantajosa quando os elementos têm poucos dígitos, como em listas de inteiros.

Comparação Teórica vs. Prática:

• Radix Sort foi um dos algoritmos mais rápidos em todos os tamanhos de dados, especialmente em listas de inteiros grandes. Sua complexidade $O(nk)$ torna-o extremamente eficiente para conjuntos de inteiros, e o fato de ele não depender de comparações permite que o Radix Sort seja, em muitos casos, mais rápido que o Quick Sort e o Merge Sort.
• Em nossos testes, o Radix Sort manteve um desempenho estável e rápido, confirmando sua vantagem para dados numéricos inteiros. No entanto, vale notar que ele não é adequado para ordenar dados de ponto flutuante ou strings sem adaptações específicas.

Os resultados práticos confirmam que o Radix Sort é uma excelente escolha para listas de inteiros grandes e que sua complexidade linear o torna uma das opções mais rápidas para esses tipos de dados. No entanto, ele é menos versátil que o Quick Sort e o Merge Sort, pois não funciona tão bem para tipos de dados mais complexos.

Resumo Comparativo: Teoria vs. Prática

A análise dos resultados práticos em relação à complexidade teórica mostra que:

• Algoritmos $O(n^2)$ são viáveis apenas para listas pequenas. Em listas grandes, seu tempo de execução se torna proibitivo.
• Algoritmos $O(n \, log \, n)$ como Quick Sort e Merge Sort são adequados para a maioria dos casos e apresentam desempenho consistente em listas de diferentes tamanhos.
• Radix Sort se destaca como uma opção de alta performance para listas de inteiros, mas é mais limitado em termos de tipos de dados que pode ordenar.

Esses resultados reforçam a importância de escolher o algoritmo de ordenação correto com base no tipo e tamanho dos dados. Embora a complexidade teórica forneça uma boa estimativa inicial, testes práticos são essenciais para confirmar qual algoritmo é realmente o mais rápido para um caso específico.