Entendendo o Problema da Mochila Fracionária: Um Algoritmo Guloso
Entenda o Problema da Mochila Fracionária e como um algoritmo guloso pode resolver esse desafio clássico de otimização. Veja exemplos práticos, passos do algoritmo e uma implementação em Python para maximizar o valor com eficiência.

O Problema da Mochila Fracionária é um clássico dos problemas de otimização, e ele é o tipo de problema que a gente consegue resolver com eficiência usando um algoritmo guloso. Esse "fracionário" no nome está lá porque, diferentemente do problema da Mochila 0/1, a gente pode pegar frações dos itens. Ou seja, nada de “tudo ou nada”: dá para pegar só uma parte de um item, se isso for vantajoso. Vou detalhar aqui como esse problema funciona e por que a abordagem gulosa resolve ele de forma ótima.
O Problema
Esse tipo de problema aparece bastante em situações práticas. Dá para usar esse conceito em áreas como logística e investimentos. Imagine, por exemplo, uma empresa que precisa preencher caminhões com cargas de diferentes valores e pesos. O objetivo é maximizar o lucro, mas sem exceder o peso máximo do caminhão. Outro exemplo é um investidor que quer distribuir seu capital entre ativos para maximizar o retorno e, ao mesmo tempo, precisa poder investir frações do dinheiro em cada ativo.
Vamos visualizar isso assim: tenho uma mochila com uma capacidade máxima de peso e uma lista de itens. Cada item tem:
- Valor (∈): quanto ele vale.
- Peso (w): o peso dele.
O objetivo é preencher a mochila com uma combinação de itens (ou frações deles) para maximizar o valor total sem ultrapassar a capacidade de peso.
Considere o seguinte exemplo:
- Capacidade da mochila: 50 kg
- Itens disponíveis:
- Item A: Valor = 60, Peso = 10
- Item B: Valor = 100, Peso = 20
- Item C: Valor = 120, Peso = 30
Queremos a combinação desses itens que maximize o valor total dentro dessa capacidade de 50 kg.
A Abordagem Gulosa
Um algoritmo guloso toma a decisão que parece melhor a cada etapa, tentando resolver o problema como um todo. No caso do Problema da Mochila Fracionária, isso funciona bem porque posso pegar frações dos itens. Basicamente, com a estratégia gulosa, eu vou escolher sempre os itens com a maior proporção valor/peso primeiro. Em outras palavras, eu priorizo os itens que me dão mais valor por unidade de peso.
Passos do Algoritmo Guloso
Vamos ver o cálculo da razão valor/peso para cada item:
| Item | Valor (v) | Peso (w) | Valor/Peso (v/w) |
|---|---|---|---|
| A | 60 | 10 | 6 |
| B | 100 | 20 | 5 |
| C | 120 | 30 | 4 |
-
Calculo da Razão Valor/Peso para Cada Item
- Item A: 60 / 10 = 6
- Item B: 100 / 20 = 5
- Item C: 120 / 30 = 4
Assim, temos as razões em ordem decrescente: A (6), B (5), C (4).
-
Ordenar os Itens Pela Proporção
Ordenando os itens, ficamos com a sequência: A, B, C.
-
Selecionar os Itens
Agora, é só ir adicionando os itens até atingir a capacidade da mochila:
- Adiciono o Item A inteiro (peso = 10 kg), acumulando valor: 60. Capacidade restante: 50 - 10 = 40 kg.
- Adiciono o Item B inteiro (peso = 20 kg), acumulando valor: 160. Capacidade restante: 40 - 20 = 20 kg.
- Finalmente, adiciono uma fração do Item C. Com 20 kg restantes e o item pesando 30 kg, pego apenas 20/30 do Item C, o que equivale a 2/3 do valor total do item: (120 * 20/30) = 80.
-
Valor Total
O valor total na mochila é: 60 (Item A) + 100 (Item B) + 80 (fração do Item C) = 240.
Complexidade do Algoritmo
É interessante entender como o algoritmo se comporta conforme o número de itens cresce, o que é essencial para prever a eficiência dele em cenários reais.
- Ordenação dos Itens: Ordenar pela razão valor/peso tem complexidade O(n log n), onde n é o número de itens.
- Selecionar os Itens: Após ordenar, percorro a lista apenas uma vez para adicionar os itens, com complexidade O(n).
Assim, a complexidade total do algoritmo é O(n log n), por conta da ordenação.
Por Que o Algoritmo Guloso Funciona?
O Problema da Mochila Fracionária é perfeito para um algoritmo guloso porque ele possui:
- Subestrutura ótima: A solução ótima para o problema pode ser composta por soluções ótimas para subproblemas menores.
- Escolha gulosa: Escolher sempre a maior proporção valor/peso resulta numa solução ótima.
Por outro lado, o Problema da Mochila 0/1 não pode ser resolvido com um algoritmo guloso, pois as melhores escolhas locais nem sempre levam à solução ótima.
Visualização Gráfica
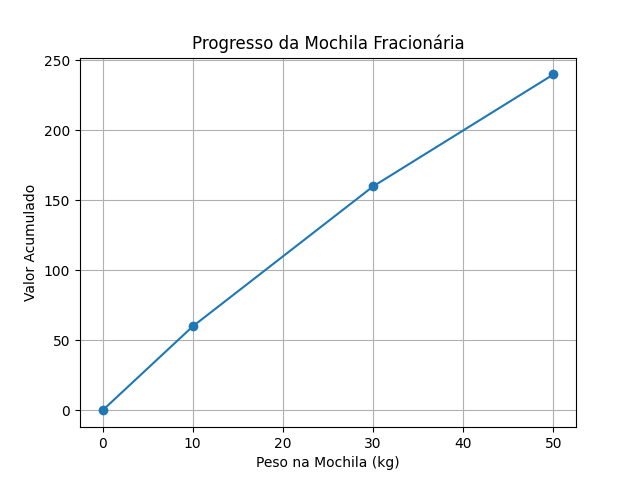
Vou adicionar uma imagem aqui depois, mostrando o progresso da mochila fracionária em um gráfico com o peso na mochila no eixo x e o valor acumulado no eixo y.
1import matplotlib.pyplot as plt 2 3pesos = [0, 10, 30, 50] # Pesos acumulados 4valores = [0, 60, 160, 240] # Valores acumulados 5 6plt.plot(pesos, valores, marker='o') 7plt.xlabel('Peso na Mochila (kg)') 8plt.ylabel('Valor Acumulado') 9plt.title('Progresso da Mochila Fracionária') 10plt.grid(True) 11plt.show()
Esse gráfico ajuda a visualizar como o valor acumulado aumenta conforme adiciono os itens na mochila.
Esse é um exemplo clássico de como algoritmos gulosos podem resolver problemas de otimização de forma eficiente. Ao sempre escolher o item com maior proporção valor/peso, garantimos a solução ótima e mantemos o processo simples e rápido. Em contraste, problemas como a Mochila 0/1 e o Caixeiro Viajante muitas vezes precisam de abordagens mais complexas porque as decisões locais não levam necessariamente à melhor solução global.